Bayesian Learning

Bayesian Ferderated Learning

• Current data-driven artificial intelligence algorithms are extremely dependent on the size of training data. Edge computing devices, such as smartphones and IoT devices, have a lot of data suitable for training models, but can’t be accessed due to current legal restrictions and public privacy concerns. To address this problem, Federal Learning focuses on training powerful models without accessing client data.

• There are many problems facing the current federal learning application process. One of them is that client data is not Independently Identically Distributed (non-i.i.d.). The current popular algorithm for federation learning, FEDAVG, is unable to perform in this case and is still some distance away from being practical.

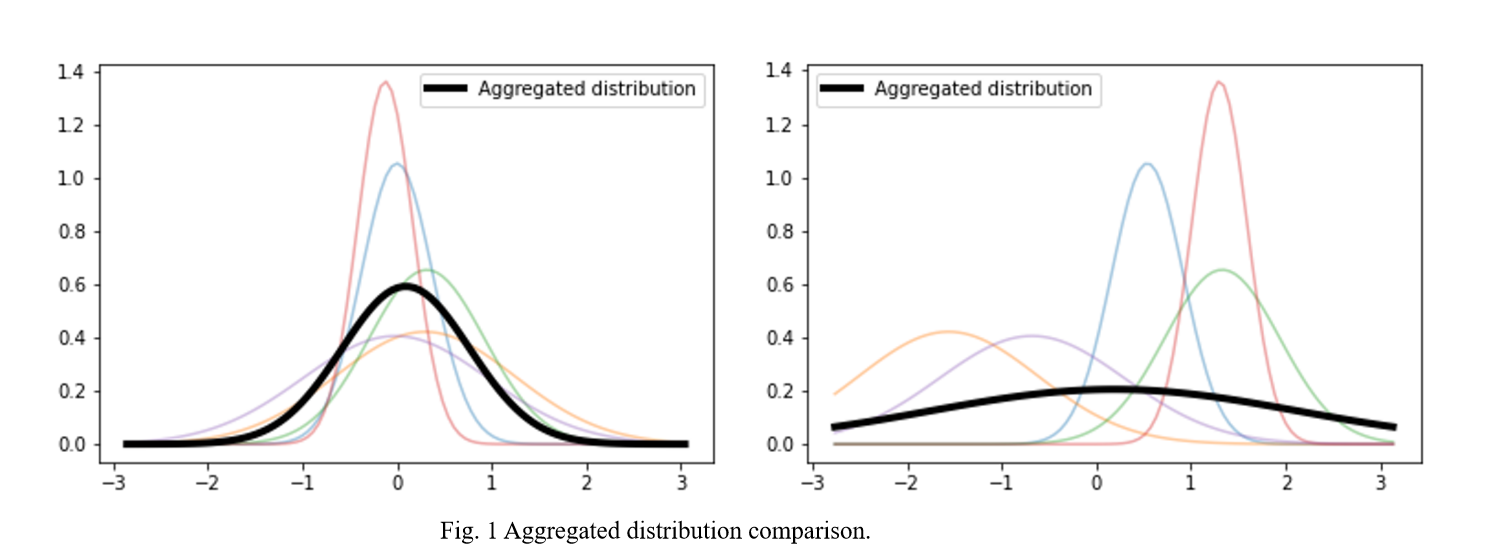
• When we analyze the FEDAVG algorithm, we can find that FEDAVG is inherently unable to handle the disagreement in the clients’ models because FEDAVG discards the variance information of the clients’ models in the aggregation parameter stage, which reflects the disagreement among clients created by the non-i.i.d. Dataset.

• The difference between a Bayesian neural network (BNN) and a point estimation neural network is that a BNN treats the parameters as distributions rather than as some fixed value. The distribution will be more informative compared to a single point. Therefore BNN can effectively preserve the disagreement between client models. BNNs will allow client models to explore alternative possibilities and thus not be limited to the optimum generated by their own database.

Bayesian Graph Convolution Networks

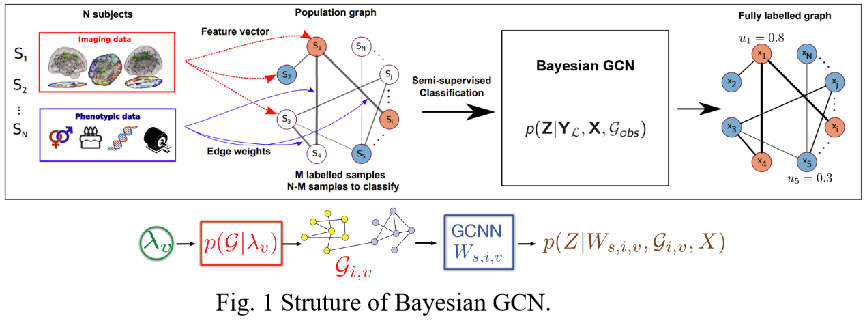
• Recently, Graph Convolutional Networks (GCNs) have been used to address node and graph classification and matrix completion. Brain disease prediction, which requires graph representation, also achieved effective results using the GCN. However, the current implementations have limited capability to incorporate uncertainty in the graph structure. Bayesian-GCN views the observed graph as a realization from a parametric family of random graphs. It targets inference of the joint posterior of the random graph parameters and the node (or graph) labels using Bayes’ theorem.

• Compared to previous GCNs, the main difference is that when we do node label prediction we simultaneously learn a graph generation model based on the observed underlying topology, and we learn the parameters of this graph generation model. We can sample several similar distributions but diverse topologies based on the posterior of the graph generation model. Thus, in the aggregation step of the GCNs, we can learn more general node embeddings by incorporating information from different potential neighbors.

• For brain disease prediction, Resting-state functional magnetic resonance imaging (rs-fMRI) is transferred to Functional Connectivity (FC) using the Pearson correlation matrix and then vectorized for the subject feature vector. The phenotypic data (age, gender, gene expression, etc.) are normalized for similarity measures between subjects. The population graph from both brain imaging data and phenotypic data will feed into Bayesian GCN for prediction and uncertainty measure.

• The Bayesian-GCN can not only be applied to graph-based rs-fMRI brain data, but also to many other applications with graph representations, e.g. biomedical area gene-gene or protein-protein interaction graphs, brain Region of Interest (ROI) connection graphs, and traditional area citation networks, social dynamic road networks. For traditional image and text tasks that can construct graph representations, Bayesian-GCN also replies with a better uncertainty measure avoiding structure flaws.